你的宠物比你想象的更会算术?揭开动物算术能力的神秘面纱
想象一下,
你有只会算数的宠物,你会做些什么?
网友A:岂不是孩子的小学算术题可以让我家宠物帮忙检查了?
网友B:再附加教算术的技能,最好有大学高数的水平

网友C:太棒啦!我要让我家宠物去当网红!!!

网友D:还是你会想.......
在某视频平台上,真有一只会算数的小猪,名叫奇奇(账号名为“小猪奇奇会算数”)。他的主人提出5以内加减法的题目,奇奇就会用嘴巴从面前的几个卡片中叼起写有正确答案的卡片。
网友A:什么?!世界上竟真有
会算数的猪?!
网友C:这不就是我的梦中情猪吗,
会做高数题的升级版给我来一打!!
网友B:.........冷静盆友

这究竟是主人的把戏,还是动物果真有如此聪慧?是真是假,就让我们来为各位客官们拨开迷雾。

小猪做算术题(图源:清华“智谱清言”AI生成)
从马戏团到实验室
会算数的动物其实早在20世纪初期就有出现了。一位叫做威廉·冯·奥斯滕(Wilhelm Von Osten)的德国马戏团驯兽师名扬一时,这有赖于他的得意搭档——一匹名叫汉斯(Hans)的马。起初,汉斯只是能够解决一些简单的加法问题,例如,当主人在两张桌子上分别摆放5件和3件物体时,汉斯就会用蹄子敲击地面8次,作为对5+3这个问题的回答。随着名气的增长,汉斯的能力也与日俱增,他甚至能够对黑板上用阿拉伯数字书写的如2/5+1/2这样的复杂问题给出正确的答案——先用蹄子敲9下,然后再敲10下,表示9/10。

聪明的汉斯在进行表演(图源:维基百科)
汉斯的神奇能力引起了心理学家们的怀疑,一位名叫奥斯卡·芬格斯特(Oskar Pfungst)的研究者提出假设:汉斯可能并不是真的理解了算数问题,而是主人在其敲击到正确次数时给了汉斯隐蔽的提示,让汉斯停止敲击。
为了验证这一假设,他先把算数问题只呈现给主人,再把题板转向汉斯,在部分试次中,题板上的题目会悄悄被换掉——此时主人并不知道汉斯所看到的题目已经和他自己刚刚看到的有所不同。结果显示,当主人不知道汉斯所看的题目时,汉斯就无法给出正确的答案。这一项简单的实验有力地证实了芬格斯特的假设。今天,心理学上将实验者预期对实验对象(无论是人还是动物)行为的影响称作“观察者预期效应”或“聪明的汉斯效应”。
回到开头提到的“小猪奇奇”,我们不难推断,小猪很有可能也是在受到了主人隐蔽的提示后才选出了正确的答案。
网友C:小猪奇奇和汉斯不是一个物种啦!!!!!

网友D:你说的很有道理,
所以只有严谨的科学实验,
才能真正解开动物的计算能力之谜。

No.1:动物眼中的数量和我们一样吗
在探讨动物的计算能力之前,我们有必要首先考察的一个问题是:动物能否像我们一样认识数量?
一个简单的实验设计被称为“延迟匹配到数量任务”(delayed match-to-numerosity task, DMNT)。实验者首先给人或动物呈现包含一定数量的点的图案,接着,图案消失一段时间,再呈现一个新的图案——如果新的图案与之前的图案包含相同数量的点,受试则需要按键,在规定时间内的按键会带来食物(对于动物)或金钱(对于人类)的奖励。相反,当呈现的图案包含的点的数量与之前不同时,受试需要“忍住”不去按键,直到一段时间之后屏幕上会呈现一个必定与之前包含相同数量的点的图案,这时,我们的受试们就可以去按键获取奖励了。
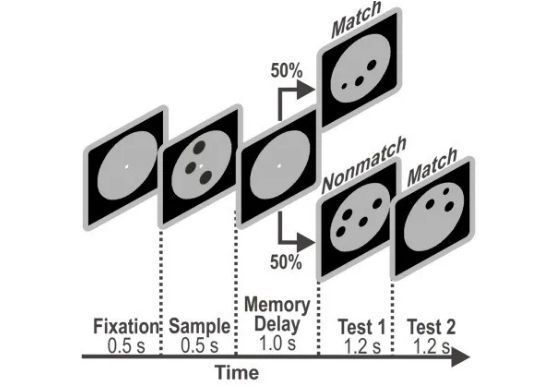
DMNT实验设计(图源:Nieder, 2020)
实验结果清晰地显示出,无论是乌鸦、猕猴还是人类(由于呈现时间短,人类没有足够的时间进行逐个数数),随着点的数量的增加,他们对数量的分辨率都开始下降。
回想一下你自己生活中的经验,
你想买3个苹果,
而售货员只拿给你2个
你:

但如果你买了一包花生米,
包装袋上写着里面有100个,
实际只装了99个,
你能发现吗?
卖家:人家不是有意的,嘤嘤嘤

对于这种模糊的数量感知,神经科学家斯坦尼斯拉斯·迪昂(Stanislas Dehaene)给出了一个形象的比喻:蓄水池隐喻。他假想流落荒岛的鲁滨逊为了计数土著人的数量,搭建了一个简易的蓄水池,每次有一个土著人到来,鲁滨逊便向蓄水池中蓄注一些水,这样,水面的高度就代表了土著人的数量。然而,由于没有准确的量具,他每次蓄水的体积在一定范围内波动。如此一来,蓄水1次和蓄水2次的水位显然有着明显的不同;但当需要计数的数量变得较大,蓄水9次和蓄水10次后的水面高度就可能难以区分了。

鲁滨逊向蓄水池中蓄水(图源:清华“智谱清言”AI生成)
除了行为上的证据,研究者们还在猴的大脑的前额叶脑区(这里常常被认为与各种高级的脑功能有关)中发现了表征数量的神经元。与行为上的结果相一致,这些神经元虽然对特定的数量活动最多,对其相近的数量也表现出一定水平的活动。
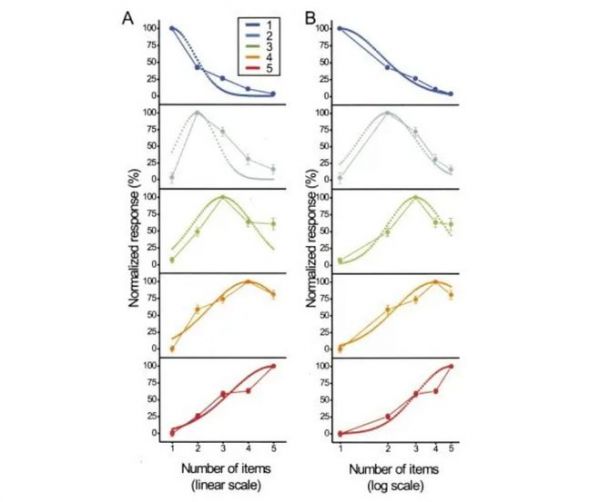
数量表征神经元对不同数量的活动水平。A图横轴为线性标尺,B图横轴为对数标尺。可以看到,对数标尺下数量神经元对活动水平与数量的关系更符合方差相同的正态分布,这与数量越大分辨率越低的行为结果相统一 (图源:Nieder and Earl, 2003)
No.2:动物的数学水平能通过练习提高吗?
别走!这是最后一步!!
我发誓!!!
文末还有一则好消息!

在证明了动物对数量有不精确的感知能力之后,是时候给他们真正的数学题考验了。不过,如何让他们理解题目的含义呢?
Cantlon等人设计了一个巧妙的实验:他在屏幕上先呈现一个圆点,接着,一个大方块从屏幕上方降下,盖住圆点,然后,另一个圆点从屏幕侧方出现,藏进方块的背后,这一过程就代表了1+1。最后,包含不同圆点数量的两个选项呈现在猴子面前,猴子只有选出正确的数量(2)才能得到他喜爱的果汁。如果是减法,则是减数个圆点先被方块盖住,然后有减数个圆点从方块后面飞出来。整个过程完全在计算机的控制下完成,不需要实验员在场,这很好地避免了“聪明的汉斯效应”。
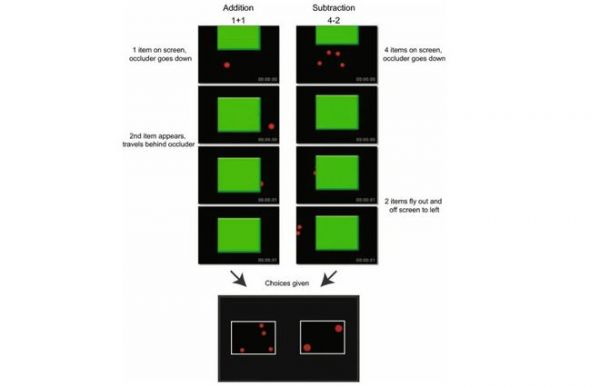
形象化的加减法问题呈现(图源:Cantlon et al., 2016)
实验发现,猴子能够以显著高于随机的水平选出正确的答案,然而,他们的正确率似乎存在一个难以逾越的瓶颈。在长达三年的练习中,本实验所用的两只猴子都未能表现出正确率升高的趋势。其根本的障碍很可能来源于他们不精确的数量感知。如果猴子永远把“4”看成“一个最有可能是4,还有可能是3或5,不大可能是2或6的数量”,又如何奢求他们能够精确地完成加减法呢?
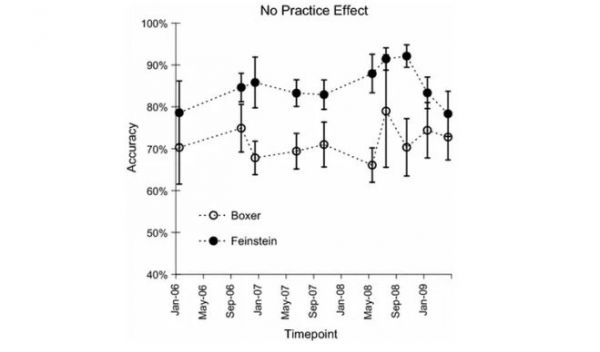
两只猴子在3年中计算正确率的变化(图源:Cantlon et al., 2016)
人脑中也有一个“动物数学系统”
作为人类,我们显然不会像猴子一样被十以内加减法难住。我们不仅能够以几乎100%的正确率完成简单的算数运算,还可以理解更多复杂而精确的数学概念。可是,这并不意味着我们已经完全抛弃了动物脑中的那套模糊、不精确的数学系统——科学家们将这种对数量的模糊感知称为“数感”(number sense)。
有许多实验上的证据表明了人类“数感”系统的存在,上文提到的“延迟匹配到数量任务”即是一例。另一个有趣的现象被称为“距离效应”:当人类被要求比较一个两个数字的大小时,人们的反应时间和错误率总是随着两个数量距离的减小而增加——比较71和65的大小要花费的时间比比较79和65花费的时间要长得多,尽管从理论上,我们只要看到十位数字是7就可以直接判断其比65更大而无需再比较个位。这似乎提示着,我们在面对数字时,脑中仍然会激起其作为一个“模糊的量”的概念。
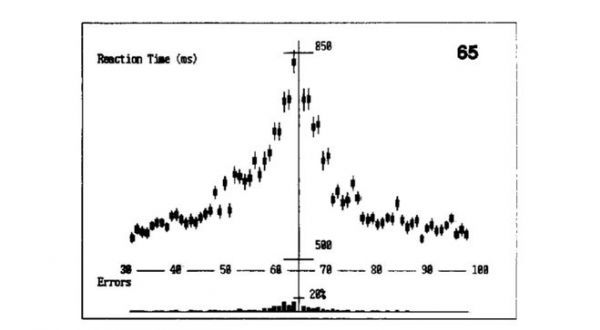
人类受试比较一个数字与65的大小所用的反应时和错误率(图源:Dehaene et al., 1990)
继承自动物的数感系统,与人类独有的精确数学系统相互配合,缺一不可,共同铸造了人类高超的数学能力。在罕见的情况下,脑部的损伤可能会造成某一系统功能的丧失,这样的患者会表现出独特的障碍:丧失精确数学系统的病人需要几秒钟的时间才能读出数字7或8,但却可以立刻判断出8比7大;而失去模糊数感的病人难以判断5和6哪个更大,却可以立刻计算出5×6=30。
最后最后,好消息来了!!!

数学渣渣们有救啦!
近年来,人们通过脑电图(EEG)、功能磁共振成像(fMRI)等脑成像方法,逐步揭示了数学能力背后的神经机制。在人类学习和成长的过程中,与数学相关的神经基础也在不断地成熟完善,人们甚至可以根据脑成像的结果预测儿童的数学成绩。
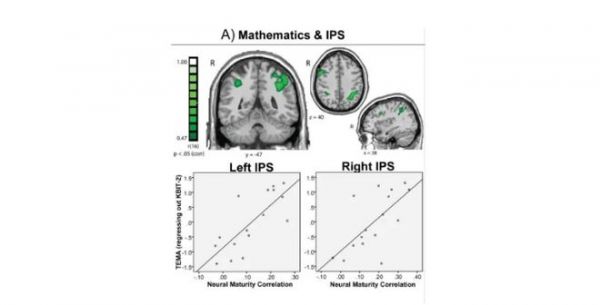
儿童在观看影片时顶内沟(IPS)脑区的神经活动与成人对应脑区活动的相似性与其在数学测验上的成绩正相关(图源:Cantlon and Li, 2013)
也许有一天,对数学神经基础的认识将帮助人类(尤其是那些面临数学学习困难的孩子们)更好地掌握数学。
网友:这得等到何年马月呀,我怕是无福消受了,小编你欺骗了我的感情。

能看到这里都是真爱,小编爱你们啦。

参考文献
[1] [法]斯坦尼斯拉斯·迪昂. 脑与数学[M].周加仙等, 译. 杭州: 浙江教育出版社, 2022.
[2] Nieder, Andreas. “Absolute Numerosity Discrimination as a Case Study in Comparative Vertebrate Intelligence.” Frontiers in psychology vol. 11 1843. 7 Aug. 2020, doi:10.3389/fpsyg.2020.01843
[3] Nieder, Andreas, and Earl K Miller. “Coding of cognitive magnitude: compressed scaling of numerical information in the primate prefrontal cortex.” Neuron vol. 37,1 (2003): 149-57. doi:10.1016/s0896-6273(02)01144-3
[4] Cantlon, Jessica F et al. “Monkeys display classic signatures of human symbolic arithmetic.” Animal cognition vol. 19,2 (2016): 405-15. doi:10.1007/s10071-015-0942-5
[5] Dehaene, S et al. “Is numerical comparison digital? Analogical and symbolic effects in two-digit number comparison.” Journal of experimental psychology. Human perception and performance vol. 16,3 (1990): 626-41. doi:10.1037//0096-1523.16.3.626
[6] Cantlon, Jessica F, and Rosa Li. “Neural activity during natural viewing of Sesame Street statistically predicts test scores in early childhood.” PLoS biology vol. 11,1 (2013): e1001462. doi:10.1371/journal.pbio.1001462
转载内容仅代表作者观点
不代表中科院物理所立场
如需转载请联系原公众号
原标题:动物会算术吗
来源:探臻科技评论
编辑:鱼非我
1.2.
3.
4.
5.
6.
7.
8.
9.
10.
相关知识
宠物狗的算术智慧(从数学角度探究狗狗智商的奥秘)
猫咪会说话的秘密(揭开宠物语言的神秘面纱)
荷兰猪:揭开萌宠的神秘面纱
鹦鹉怎么说话的秘密是什么,揭开它们语言能力的神秘面纱
为什么猫喜欢爬高(揭开猫咪喜欢攀爬的神秘面纱)
鹦鹉是怎么说话的?揭开它们语言的神秘面纱,探索交流的奥秘
探秘猫咪眼,揭开宠物世界的神秘面纱(瞳孔大小决定一切)
三花猫的智慧之谜:揭开它神秘面纱,让你欲罢不能!
小学趣味数学课:扑克牌玩24点算术游戏
兔子是杂食动物吗?揭开兔子食谱的神秘面纱
网址: 你的宠物比你想象的更会算术?揭开动物算术能力的神秘面纱 https://m.mcbbbk.com/newsview1057911.html
| 上一篇: 梦幻西游石猴授徒攻略,梦幻西游石 |
下一篇: 宠物日常猴子多少钱一只训练哪里可 |
